Через каждое ребро тетраэдра проведена плоскость, параллельная противоположному ребру. Найти отношение объема полученного параллелепипеда к объему тетраэдра.

Пусть A1BC1D-данный тетраэдр, ABCDA1B1C1D1 - параллелепипед, полученный указанным построением. Легко сообразить, что ребра тетраэдра являются диагоналями боковых граней параллелепипеда.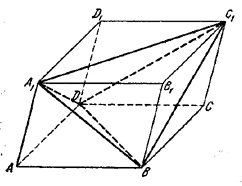


Тетраэдр может быть получен удалением из параллелепипеда четырех равновеликих пирамид: ABDA1 , BDCC1 , А1В1С1В и A1D1C1D. Так как объем каждой из пирамид, очевидно, равен 1/6 объема параллелепипеда, то отношение объема Vn параллелепипеда к объему VT тетраэдра равно





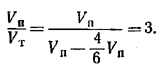
Похожие примеры:
Доказать, что для объема произвольного тетраэдра V справедлива формула \(V = \frac{1}{6}abd sin\phi\), где а и b — два противоположных ребра тетраэдра, d — расстояние между ними, \(\phi\) — угол между ними. Смотреть решение→
В правильном тетраэдре SABC с ребром основания а проведены три плоскости, каждая из которых проходит через одну из вершин основания тетраэдра ABC и середины двух боковых ребер. Найти объем части тетраэдра, расположенной над всеми секущими плоскостями.  Смотреть решение→
В пирамиде SABC произведения длин ребер каждой из четырех граней равны одному и тому же числу. Длина высоты пирамиды, опущенной из S на грань АВС, равна \(2\sqrt{\frac{102}{55}}\), а величина угла CAB равна \(arccos(\frac{1}{6}\sqrt{\frac{17}{2}})\). Найти объем пирамиды SABC, если |SA|2 + |SB|2 - 5|SC|2 = 60 Смотреть решение→