На боковых гранях правильной четырехугольной пирамиды построены, как на основаниях, правильные тетраэдры. Найти расстояние между наружными вершинами двух смежных тетраэдров, если сторона основания пирамиды равна а.

Легко видеть, что наружные вершины тетраэдров лежат в вершинах некоторого квадрата. Чтобы определить длину его стороны, проведем через вершину S пирамиды и через наружную вершину А одного из тетраэдров плоскость, перпендикулярную к основанию четырехугольной пирамиды.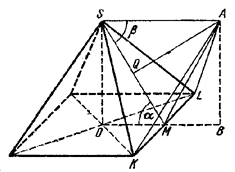

Последняя пройдет через основание О высоты пирамиды, через основание Q высоты тетраэдра и через середину М ребра KL. Опустив на плоскость основания пирамиды перпендикуляр АВ, рассмотрим четырехугольник SOBА. Его сторона ОВ является половиной диагонали упомянутого квадрата и подлежит определению. Легко, однако, обнаружить, что SOBA-прямоугольник. В самом деле, положив ∠OMS = α, ∠ASM = β, находим:

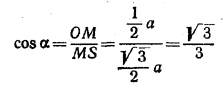
и

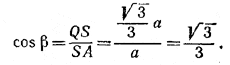
Поэтому SA и OB параллельны и, следовательно,

OB = SA= a.

Таким образом, искомое расстояние равно a√2 .