Через некоторую точку диагонали куба с ребром а перпендикулярно к этой диагонали проведена плоскость. 1) Выяснить, какая фигура получается в сечении этой плоскости с гранями куба. 2) Найти длины отрезков, получающихся в сечении плоскости с гранями куба, в зависимости от расстояния х секущей плоскости от центра симметрии куба О.
Предположим, что секущая плоскость проведена через некоторую точку диагонали HP данного куба.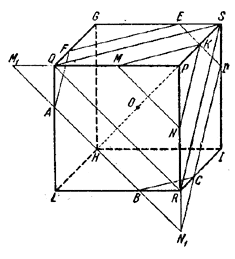
Рассмотрим сначала те сечения, которые пересекают диагональ в точках отрезка ОР. Выделим сечение QRS, проходящее через три вершины куба; оно, очевидно, принадлежит рассматриваемой совокупности. Это равносторонний треугольник со стороной a√2 . Нетрудно вычислить, что расстояние данного сечения от центра куба равно 
. Очевидно, что при 
в сечении получаются равносторонние треугольники. Так как отношение сторон рассматриваемых треугольников равно отношению их расстояний до точки Р, то
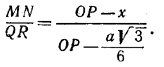
Отсюда, принимая во внимание, что 
, находим:
MN =3/2√2а - х √6. (1)
Если же 
, то в сечении получаются шестиугольники ABCDEF.
Стороны шестиугольника АВ, FE и CD соответственно параллельны сторонам QR, QS и RS равностороннего треугольника QRS. Поэтому при продолжении, пересекаясь, они образуют углы в 60°. Учитывая еще, что AF || CD и т. д., мы приходим к заключению, что все углы шестиугольника равны 120°. Легко видеть также, что AB = CD = EF и BC = DE = AF (следует принять в расчет, что стороны шестиугольника отсекают на гранях равнобедренные треугольники).
Для того чтобы найти длины сторон шестиугольника, продолжим сторону АВ шестиугольника до пересечения в точках М1 и N1 с продолжениями ребер PQ и PR. Длина отрезка M1N1, может быть, очевидно, вычислена по формуле (1). Зная M1N1 находим отрезок
BN1 = ( √2/2 M1N1 - a ) √2 = a/2√2- x√6
Отсюда
AB = M1N1 - 2BN1 = a/2√2 + x√6. (2)
Сторону ВС можно было бы определить аналогично. Нетрудно, однако, сообразить, что BC = BN1и, следовательно,
BC = a/2√2- x√6. (3)
Отметим, что в сечении с плоскостью π, проходящей через точку О, получается правильный шестиугольник (см. формулы (2) и (3) при x= 0). Вершины этого шестиугольника лежат в серединах ребер куба.
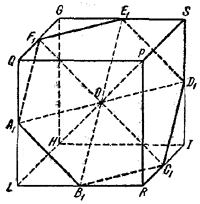
Легко видеть, что если одну из двух частей, на которые плоскость πразбивает куб, повернуть на 60° около диагонали ОР, то шестиугольник совпадает с самим собой, и мы получим два симметрично расположенных относительно плоскости π многогранника. Следовательно, сечение, пересекающее диагональ в точках отрезка НО на расстоянии х от точки О, получается из соответствующего сечения уже рассмотренной совокупности секущих плоскостей поворотом на 60°.