Ребро куба равно а; АВ — его диагональ. Найти радиус сферы, касающейся трех граней, сходящихся в вершине А, и касающейся трех ребер, выходящих из вершины В. Найти также часть поверхности этой сферы, которая лежит вне куба.
Центр О шара (рис.) лежит на диагонали АВ. Действительно, точка О одинаково удалена от граней AA1N1N и AA1Q1Q. Значит, она лежит на плоскости, делящей пополам двугранный угол при ребре АА1. Таким же образом точка О должна лежать на плоскости, делящей пополам двугранный угол при ребре AN. А эти две плоскости пересекаются по диагонали АВ.
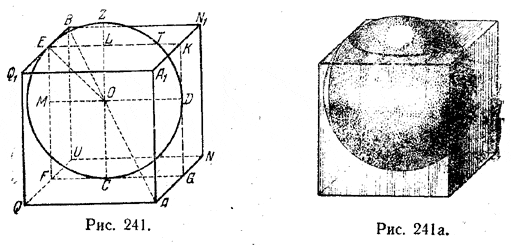
Пусть С и D - точки касания шара с гранями ANUQ и AA1N1N, а r - радиус шара. Тогда OC=OD= r, и плоскость ODGC перпендикулярна к ребру AN, а также к ребру BQ1
Так как ребро SQ1 по условию касается шара, то плоскость ODGC пересечет ребро в точке Е его касания с шаром; следовательно, ОЕ= r. С другой стороны, точка Е есть вершина квадрата FGКЕ, получаемого в сечении куба плоскостью ODGC; значит четырехугольник MOLE (OL и ОМ - продолжения прямых ОС и OD) - квадрат. Следовательно, ОМ = r/√2. Так как OM + ОD = MD = a, то r/√2 + r = а, откуда r = (2 - √2 ) а.
Часть поверхности сферы, лежащая вне куба, состоит из трех равных сегментов, один из которых есть EZTL. Поверхность этого сегмента равна
2πr • LZ = 2πr (CZ - CL) =2πr (2r - а),
Ответ: r = (2 - √2 ) а; S = 6πa2 (10 - 7√2).