В конус вписан шар радиуса r. Найти объем конуса, если известно, что плоскость, касающаяся шара и перпендикулярная к одной из образующих конуса, отстоит от вершины конуса на расстоянии d.
Можно провести две плоскости, перпендикулярные к данной образующей конуса (СА на рис.) и касающиеся вписанного шара; их точки касания (N и N1) лежат на диаметре NN1 параллельном СА.
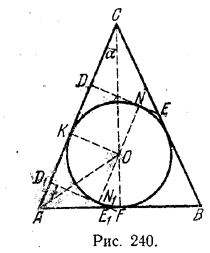
Положим сначала, что берется плоскость ND, касающаяся шарa в точке N. Четырехугольник ONDK (К - точка касания образующей СА с шаром) - квадрат, так что DK=ON= r. По условию CD = d. Следовательно, CK= d + r. Из треугольника КОС находим
СО = √(d + r)2 + r2.
Следовательно,
Н = CF = OF + ОС = r + √(d + r)2 + r2 .
Из подобия треугольников AFC и KОС находим
AF : Н = ОК : КС,
откуда
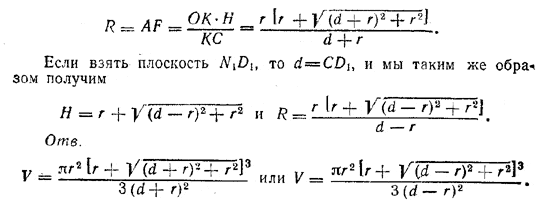
Похожие примеры: