На плоскости Р лежат три равных шара радиуса R, касающиеся друг друга. Прямой круговой конус расположен так, что его плоскость основания совпадает с Р, а данные шары касаются конуса и лежат вне его. Найти радиус основания конуса, если его высота задана и равна qR.
Обозначим через r искомый радиус основания конуса. Рассмотрим фигуру, получающуюся в сечении, проведенном через центр одного из шаров и ось конуса.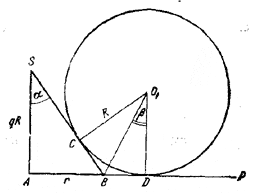
Заметим, что расстояние между центрами двух касающихся шаров равно 2R. Используя легко доказуемый факт, что центр основания конуса А расположен на одинаковом расстоянии от всех трех точек касания сфер с плоскостью Р, находим:
Легко видеть, что ∠SB A = ∠СО1О = 2β и, следовательно,
2β = π/2 - α
Взяв тангенсы углов, стоящих в обеих частях этого равенства, получаем:
(1)
Из рис. видно, что 
Если теперь положить r/R = х , то равенство (1) приведет нас к следующему уравнению относительно х :
3(q - 2) х2 - 4√3 (q - 1) х + q= 0.
Отсюда при q = 2 получаем х = √3/6, следовательно, r =√3/6 R. Если же q =/=2, то
Так как 
то в указанной формуле следует взять знак минус. Второй корень при q > 2, как нетрудно показать, больше, чем 
, и отвечает конусу, касающемуся сфер извне; при q < 2 второй корень отрицателен.