Даны четыре равных шара радиуса R, из которых каждый касается трех других. Пятый шар касается каждого из данных шаров внешним образом, шестой — внутренним образом. Найти отношение объема шестого шара V6 к объему пятого V5.
Центры четырех первых шаров лежат в вершинах правильного тетраэдра, так как расстояния между центрами любых двух касающихся шаров равны 2R. Нетрудно показать, что центры пятого и шестого шаров совпадают с центром тяжести тетраэдра.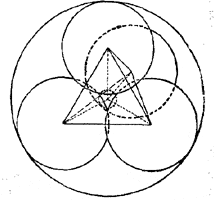
Пусть r - радиус пятого (большего) шара, а ρ - радиус шестого шара. Очевидно,
r = ρ + 2R. (1)
Пользуясь тем, что расстояние от центра тяжести до вершины рассматриваемого тетраэдра равно √6/2 Rполучаем:
ρ + R = √6/2 R. (2)
Отсюда ρ = R( √6/2 - 1 ) , а из формулы (1) r =R( √6/2 +1 ) .
Таким образом, искомое отношение объемов равно
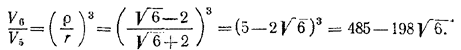
Похожие примеры: