На столе, касаясь друг друга, лежат четыре шара одинакового радиуса r. Сверху в ямку, образованную ими, положен пятый шар того же радиуса. Найти расстояние от верхней точки пятого шара до плоскости стола.

На плоскости Р (рис.) лежат четыре шара радиуса r; М, N, К и L - точки их касания с плоскостью Р.

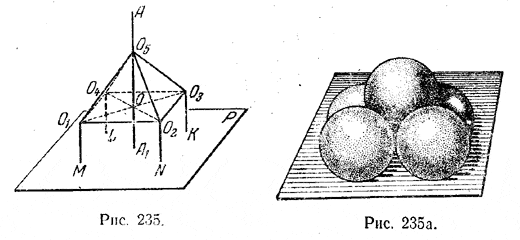
Их центры О₁,О₂,О₃,О₄ удалены от плоскости на расстояния О₁М=O₂N=O₃K=O₄L= r. Расстояние между центрами двух касающихся друг друга шаров равно 2r, т. е.
О₁О₂=О₂О₃=О₃О₄=О₄О₁ = 2r. Пятый шар касается каждого из четырех первых; следовательно, центр его О₅ удален от центров О₁ О₂, О₃, О₄ также на расстояние 2r ,т.е. O₁O₅=O₂О₅=О₃О₅=О₄О₅=2r. Поэтому фигура О₅О₁О₂О₃О₄ будет правильная четырехугольная пирамида, у которой все ребра равны (как при основании, так и боковые). Центр пятого шара будет удален от плоскости Р на расстояние, равное OO₅+ ОА₁ = ОО₅+r. Верхняя точка А пятого шара будет находиться на продолжении перпендикуляра А₁О₅ на расстоянии О₅А= r от центра O₅. Таким образом, расстояние АА₁ от верхней точки пятого шара до плоскости Р равно 2r + ОО₅. Отрезок ОО₅ находим из прямоугольного треугольника O₁OO₅, где

Ответ: AA₁ = r (2 + √2 ).