Даны два шара О и О1 касающиеся извне, и описанный около них конус. Вычислить боковую поверхность усеченного конуса, основаниями которого служат окружности прикосновения шаров к поверхности конуса, если радиусы шаров равны R и R1
При обозначениях рис. имеем: Sбок. = π (r + r1)l.
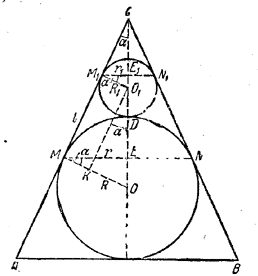
Проведем радиусы OM = R и О1M1 = R1 в точки, касания и прямую O1K, перпендикулярную к ОМ. Получим треугольники О1M1E1, ОМЕ и O1КО, которые подобны друг другу (как прямоугольные, имеющие по равному углу α). В А О1КО имеем
О1О = R + R1; OK = R - R1; O1K = MM1 = l .
Следовательно,
![]()
Из подобных треугольников ОМЕ и O1KO имеем ![]() отсюда
отсюда
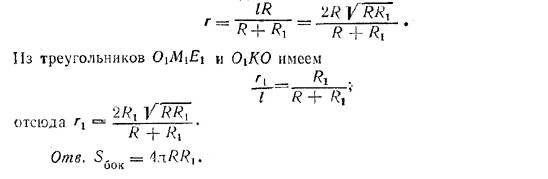
Похожие примеры: