На высоте конуса, равной Н, как на диаметре, описан шар. Определить объем части шара, лежащей вне конуса, если угол между образующей и высотой равен α.
На рис. осевое сечение той части шара, объем которой требуется определить, обозначено штриховкой.
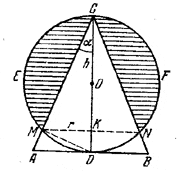
Этот объем V получается вычитанием объема V1 конуса MCN из объема V2 шарового сегмента CEMKNF. Введем обозначения: МК= r и KC = h. Так как радиус шара равен OC = 1/2CD = H/2, то
![]()
Сюда нужно подставить выражения
h =MC • cos α = H cos2 α и r = MC • sin α = H cos α sin α
(вычисление упростится, если предварительно заменить r2=МК2 через
CK • KD = h (H - h)); тогда
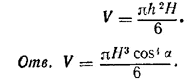
Похожие примеры: