Определить объем в полную поверхность шарового сектора, вырезанного из шара радиуса R и имеющего в осевом сечении угол α.

Обозначим (рис.) радиус шара через R, высоту DC сегментной поверхности АСВ через h и отрезок DA через r.

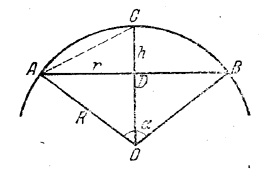
Объем V сектора равен V = ²/₃πR²h, Из треугольника ACD, где ∠ CAD =^α/₄ ( как вписанный, опирающийся на дугу ВС = ^α/₂ ), находим h = r tg ^α/₄ . Из треугольника ADO инеем r = R sin ^α/₂ . Следовательно,

V = ²/₃πR²h = ²/₃πR² • R sin ^α/₂ tg ^α/₄

Полная поверхность сектора состоит из поверхности сегмента АСВ, равной 2πRh, и боковой поверхности конуса АОВ, равной πrR. Следовательно,

S_п. = 2πRh + πrR,= πR( 2h + r).

Ответ: V = ^4π/₃ R³ sin^{2 α}/₄ ; S_п. = πR² sin ^α/₂ (2 tg ^α/₄ + 1).