Дан конус объема V, образующая которого наклонена к плоскости основания под углом α. На какой высоте надо провести плоскость, перпендикулярную к оси конуса, чтобы сечение конуса разделило пополам его боковую поверхность? Тот же вопрос для полной поверхности.

Из соотношений V = πR²H и R = H ctg α получим

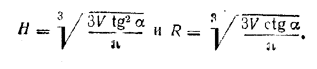
Пусть требуется разделить пополам боковую поверхность.

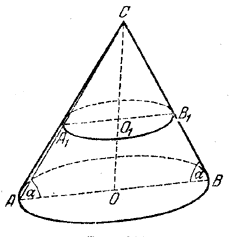
Так как конусы AВС и А₁В₁С (рис.) подобны, то их боковые поверхности S и S₁ относятся, как Н²=ОС² к H₁²=O₁C². Следовательно,

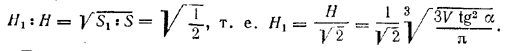
Пусть теперь требуется разделите пополам полную поверхность, Тогда

πR₁l₁ = ¹/₂π(R²+ Rl).

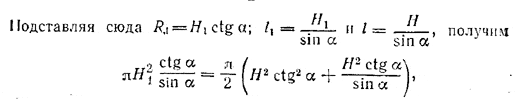
откуда H₁ = H cos ^α/₂.

Ответ: Если пополам делится боковая поверхность, то

;

если полная, то