В конус, радиус основания которого равен R и образующие наклонены к основанию под углом α/2, вписана прямая треугольная призма так, что ее нижнее основание лежит на основании конуса, а вершины верхнего — на боковой поверхности конуса. Определить боковую поверхность призмы, если в основании призмы лежит прямоугольный треугольник с острым углом α, а высота призмы равна радиусу сечения конуса плоскостью, проходящей через верхнее основание призмы.
Если радиус O1A1 (рис.) обозначить через r, то высота А1М призмы тоже равна r , а из треугольника A1B1C1, где A1B1 = 2r, имеем
A1C1 = 2r cos α и B1C1 = 2r sin α.
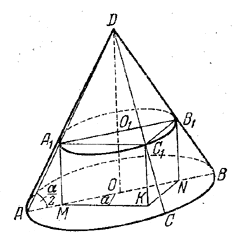
Величину r найдем из треугольника АА1М, где AM = R - r. Имеем R- r = r ctg α/2 .
Отсюда
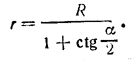
Теперь находим боковую поверхность призмы:
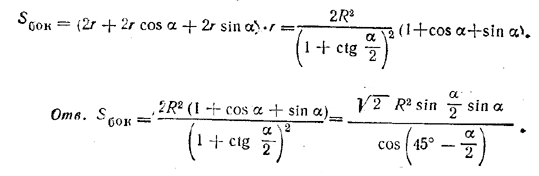
Похожие примеры: