В конус, поставленный основанием вверх и представляющий в осевом сечении равносторонний треугольник, налита вода и положен шар радиуса r. Тогда оказалось, что уровень воды касается шара. Определить высоту воды в конусе после того, как шар будет из него вынут.
На рис. изображено осевое сечение конического сосуда; ADB - уровень воды.
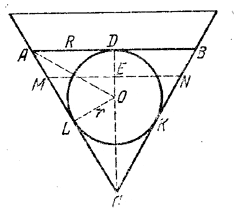
Треугольник AВС - равносторонний; круг DKL (большой круг шара) вписан в него.
При обозначениях рис. R = OD • tg 60° = r √3 и H = СD = 3r
(Радиус круга, вписанного в равносторонний треугольник, равен одной трети высоты этого треугольника; это следует из того, что точка пересечений медиан каждого треугольника делит каждой медиану в отношении 1:2).
Объем V воды в сосуде равен объему конуса ABC без объема шара, т. е.
V = 1/3 π ( R2H - 4r3 ) = 5/3 πr3
Когда шар будет вынут, вода опустится до некоторого уровня MN и заполнит конус MNC. Пусть CE = h. Тогда ME = CE • tg 30° = h/√3
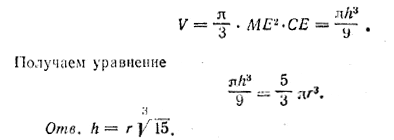
Похожие примеры: