Тупоугольный треугольник, острые углы которого α и β и меньшая высота равна h , вращается около стороны, противолежащей углу β. Найти поверхность тела вращения.
Поверхность S тела вращения равна сумме боковых поверхностей двух конусов с осевыми сечениями BAB1 , и ВСВ1.
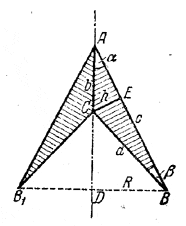
При обозначениях рис. имеем S = πRс+ πRa.
Из \(\Delta\)СВЕ имеем a = h/sin β ; по теореме синусов имеем
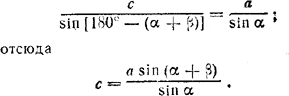
Из \(\Delta\)BCD, где ∠ BCD = α + β, имеем R = а sin (α + β). Значит,
![]()
Выражение в квадратных скобках можно преобразовать по формуле суммы синусов.
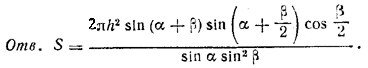
Похожие примеры: