Прямая линия — касательная к боковой поверхности конуса — составляет с образующей, проходящей через точку касания, угол θ. Какой угол φ составляет эта прямая с плоскостью основания Р конуса, если образующие его наклонены к плоскости Р под углом α?

Через точку М (рис.) боковой поверхности конуса проведена касательная прямая MB, составляющая с образующей СМА угол θ = ∠ BMA.

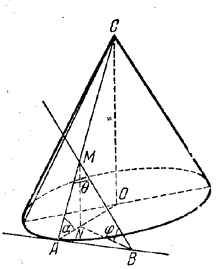
Известен еще угол α = ∠ OAM; требуется найти угол φ, образуемый прямой MB с плоскостью Р основания конуса.

Прямая MB, касающаяся конуса, пересекает плоскость в некоторой точке В, лежащей на касательной АВ к окружности основания. (Это можно доказать лишь на основе определения касательной к боковой поверхности конуса. Но такого определения в элементарной геометрии не дается).

Опустив из точки М перпендикуляр MN иа радиус ОА, получим проекцию BN прямой ВМ на плоскость Р. Значит, φ = ∠ NBM. Из \(\Delta\)AMN имеем

AM = ^MN/_{sin α}

из \(\Delta\)МAВ имеем

MB = ^AM/_{cos θ} = ^MN/_{sin α cos θ}

из \(\Delta\)MNB находим

sin φ = ^MN/_MB = sin α cos θ.

Ответ: φ = arc sin (sin α cos θ).