В конус, у которого угол осевого сечения при вершине равен α , вписан шар радиуса R. Найти объем части конуса, расположенной над шаром.
Рассмотрим осевое сечение ABC конуса. Пусть BF - высота в треугольнике ABC, N и М - точки касания круга, вписанного в треугольник ABC, со сторонами АВ и ВС, О - центр круга, Е - точка пересечения меньшей дуги MN с отрезком BF, D - точка пересечения отрезков MN и BF.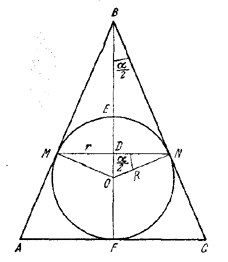
Положим DM = r, DE = H, BD = h. Искомый объем равен
V = 1/3πr2h -1/3πH2 (3R - H).
Но
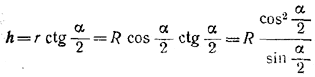
и
H = R - R sin α/2;
следовательно,
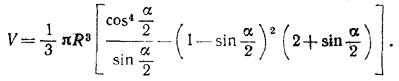
Похожие примеры: