Определить радиусы двух шаров, которые, пересекаясь, образуют двояковыпуклую линзу, если известны толщина линзы 2а, полная ее поверхность S и диаметр 2R.

Обозначим через r и r₁ радиусы шаров и рассмотрим сечение шаров плоскостью, проходящей через их центры О и О₁;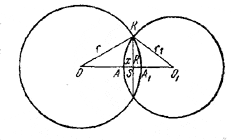

пусть АА₁ = 2а, KS = R и AS = x; тогда A₁S = 2a - x.

Полная поверхность линзы равна

2xar₁ + (2a - x)2ar = S. (1)

Из треугольника OKS имеем

r² = R² + [r - (2а - x)]²

или

R² - 2r (2а - x) + (2а - x)² = 0. (2)

Аналогично из треугольника O₁KS имеем r₁ = R² + (r₁-х)² или

R² - 2r₁х + x² = 0. (3)

Из (2) и (3) находим:

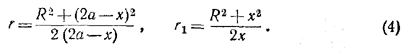
Подставив эти выражения для r и r₁ в равенство (1), получим уравнение

π(R² + х²) + π[R² + (2а - х)²] = S

или

х²- 2ах + R² + 2а² -^S/_2π= 0,

откуда

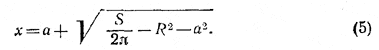
Подставив это значение х в формулы (4), после упрощений получим:

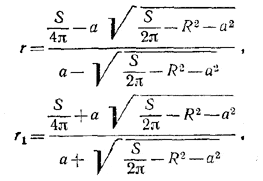
Выбор другого знака перед корнем в (5) сводится к перемене обозначений r и r₁.