В конус вписан шар, причем отношение их объемов равно k. Найти отношение объемов шаровых сегментов, отсекаемых от шара плоскостью, проходящей через линию касания шара с конусом.

Пусть V₁ и V₂ суть соответственно объемы меньшего и большего шаровых сегментов, на которые разбивает шар плоскость, проходящая через линию касания шара с конусом. Пусть, далее, R - радиус шара, h - высота меньшего сегмента, Н - высота конуса, r - радиус его основания.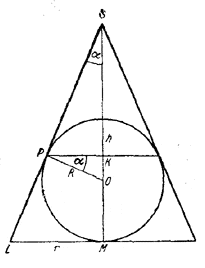

Тогда

V₁ = ¹/₃πh² (3R - h), V₂ = ⁴/₃πR³ - ^π/₃ h²(3R - h).

Задача сводится к нахождению отношения ^h/_R. Обозначив через α угол между осью конуса и образующей, из \(\Delta\)РKО находим:

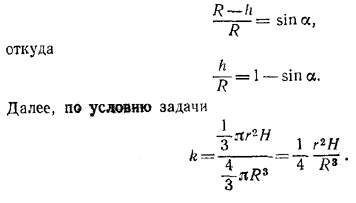
Выразим теперь r и Rчерез R и α. Имеем:

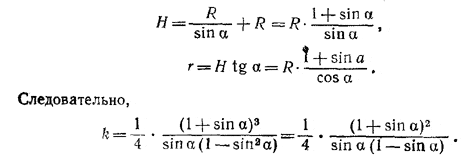
Подставляя сюда sin α = 1 - ^h/_R, получаем уравнение относительно ^h/_r= z

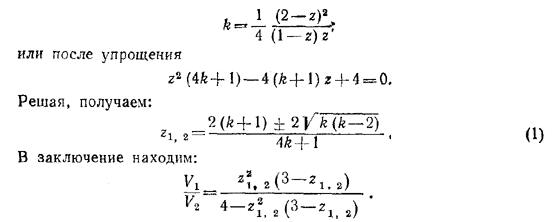
Задача имеет два решения, так как оба корня квадратного уравнения при k > 2 имеют смысл.