В сферу S радиуса R вписаны восемь сфер меньшего радиуса, каждая из которых касается двух соседних, а все вместе касаются сферы S по окружности большого круга. Затем в пространство между сферами вписана еще одна сфера S1, которая касается всех восьми сфер меньшего радиуса и сферы S. Найти радиус ρ этой последней сферы.
Радиус r каждой из восьми вписанных сфер мы найдем, рассмотрев треугольник АОС в плоскости, проходящей через центры этих сфер и центр О сферы S (рис. а).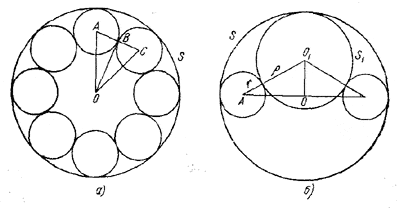
Имеем:
![]()
Отсюда
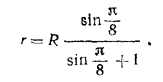
Проведя сечение через центр О сферы S, центр О1 сферы S1 и центры двух противолежащих сфер радиуса r (рис. б), мы получим из прямоугольного треугольника АОО1:
АО12 = AO2 + OO12
или
(r + ρ )2 = ( R - r )2 + ( R - ρ )2
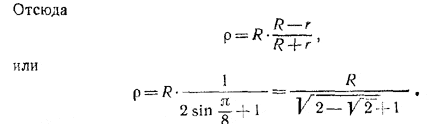
Похожие примеры: