В сферу S радиуса R вписано восемь равных сфер, каждая из которых касается трех соседних сфер и сферы S. Найти радиус вписанных сфер, зная, что их центры лежат в вершинах некоторого куба.

Так как вписанные сферы равны между собой, то их центры одинаково удалены от центра О сферы S. Следовательно, центр симметрии указанного в условии задачи куба совпадает с центром О сферы S.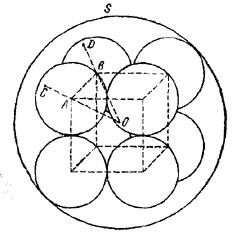

Пусть х - искомый радиус сфер. Легко видеть, что тогда ребро куба будет АВ = 2х, а половина диагонали куба

AO = CO - CA = R - x.

Так как, с другой стороны,

АО = ¹/₂•2х√3 ,

то получаем уравнение R - х = х√3 , откуда