В шар вписаны два одинаковых конуса, оси которых совпадают, а вершины находятся в противоположных концах диаметра шара. Найти отношение объема общей части этих двух конусов к объему шара, зная, что отношение высоты конуса h к радиусу шара R равно k.
Пусть r - радиус основания каждого из двух вписанных конусов. Их общая часть состоит из двух равных усеченных конусов. Обозначим через r1 и r2 соответственно радиусы верхнего и нижнего оснований усеченного конуса и через Н - его высоту. Искомое отношение объемов равно![]()
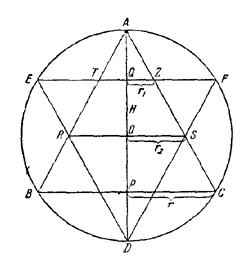
Из подобия треугольников AQZ, AOS, АРС имеем:
![]()
Так как, кроме того, H = h - R и
r = √R2- H2= √2Rh2 - h2,
то два предыдущих равенства позволяют выразить r1 и r2 через R и h:
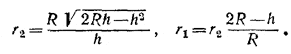
Так как по условию задачи h/R= k, то
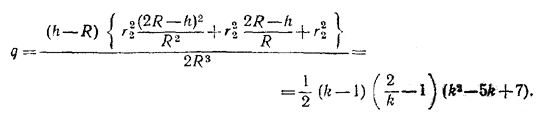
Похожие примеры: