Площади параллельных сечений шара, расположенных по одну сторону от его центра, равны S₁ и S₂, а расстояние между этими сечениями равно d. Найти площадь сечения, параллельного данным и делящего пополам расстояние между ними.

Пусть радиусы круговых сечений с площадями S₁ и S₂ равны R₁ и R₂, а расстояния от центра шара до этих сечений соответственно равны l₁ и l₂ (l₁ < l₂). Обозначим через R радиус шара, через r - радиус искомого сечения, а через l - расстояние от этого сечения до центра шара.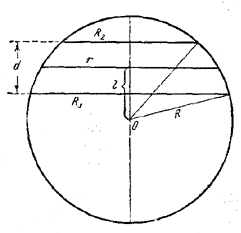

Тогда

l₂ - l₁ = d (1)

и l₁² + R₁² = l₂² + R₂² = R²

Из этих двух уравнений находим:

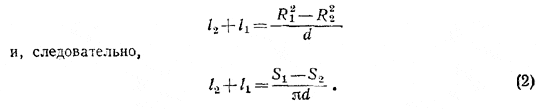
Из уравнений (1) и (2) получаем:

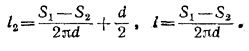
Поэтому искомая площадь равна