Дана плоскость Р и две точки А и В вне ее. Через А и В проводятся всевозможные сферы, касающиеся плоскости Р. Найти геометрическое место точек касания.
Возможны два случая:
1) Прямая АВ не параллельна рассматриваемой плоскости Р. Обозначим через D соответствующую точку пересечения АВ и Р (рис.).
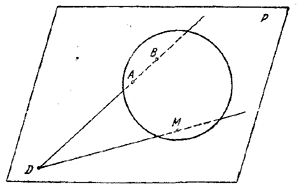
Пусть М - точка касания плоскости с одной из сфер рассматриваемой совокупности. Через прямые АВ и DM проведем плоскость. Последняя пересечет сферу по окружности, касающейся прямой DM в точке М. По известному свойству касательной и секущей, проведенных из одной точки к окружности, имеем: DB•DA = DM2. Следовательно, отрезок DM имеет постоянную длину √DB•DA, не зависящую от выбора сферы, и, значит, все точки М лежат на окружности радиуса r = √DB•DA с центром в точке D. Обозначим эту окружность через С. Пусть теперь, наоборот, М есть некоторая точка окружности С; докажем, что она принадлежит рассматриваемому геометрическому месту.
Проведем через точки А, В и М вспомогательную окружность и центр ее обозначим через О1 (рис. ниже).
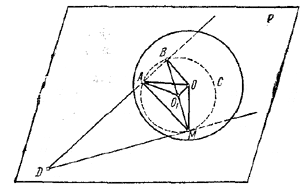
Так как в наших условиях DB•DA = DM2, то прямая DM является касательной к этойокружности и, следовательно, О1М⊥DM. Восставим теперь в точке М перпендикуляр к плоскости Р, а в точке О1 -перпендикуляр к плоскости вспомогательной окружности. Эти два перпендикуляра лежат в плоскости, перпендикулярной к прямой DM в точке М и не параллельны (в противном случае точка O1 , а вместе с ней и точки А и В оказались бы в плоскости Р). Поэтому эти перпендикуляры пересекаются в некоторой точке О. Легко видеть, что О А = OВ = OМ, ибо проекции этих отрезков О1А, О1В и О1М равны между собой как радиусы окружности. Поэтому если построить сферу с центром в точке О и радиусом ОМ, то она коснется плоскости Р и пройдет через точки А и В. Таким образом, обратно, любая точка окружности С принадлежит нашему геометрическому месту. Следовательно, искомое геометрическое место есть окружность С.
2) В случае, когда прямая АВ параллельна плоскости, искомое геометрическое место представляет собой прямую, которая лежит в плоскости Р, перпендикулярна к проекции отрезка АВ на плоскость Р и делит ее пополам.