Найти геометрическое место оснований перпендикуляров, опущенных из данной точки пространства на прямые, лежащие в заданной плоскости и пересекающиеся в одной точке.

Данную точку пространства обозначим через А, точку пересечения прямых-через В, основание перпендикуляра, опущенного из А на плоскость, - через С.

Возьмем, далее, любую прямую, проходящую через точку В, и опустим на нее перпендикуляр AD (рис.).

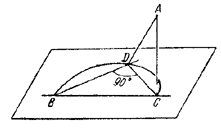
Тогда по известной теореме CD⊥BD.

Следовательно, точка D лежит на окружности, диаметром которой является отрезок ВС. Легко показать, что и, обратно, любая точка указанной окружности есть основание перпендикуляра, опущенного из точки А на некоторую прямую рассматриваемого семейства. Поэтому искомое геометрическое место есть окружность с диаметром ВС.