Дана правильная треугольная пирамида SABC (S - ее вершина). Ребро SC этой пирамиды совпадает с боковым ребром правильной треугольной призмы A1B1CA2B2S (А1А2, В1В2 и CS - боковые ребра, а А1В1С- одно из оснований). Вершины А1 и В1 лежат в плоскости грани SAB пирамиды. Какую долю от объема всей пирамиды составляет объем части пирамиды, лежащей внутри призмы, если отношение длины бокового ребра пирамиды к стороне ее основания равно \(\frac{2}{\sqrtЗ}\)?
Пусть К - середина АВ, Р - основание перпендикуляра, опущенного из К на CS. Возьмем на АВ точки М и N так, что ΔРМN - правильный (рис.).
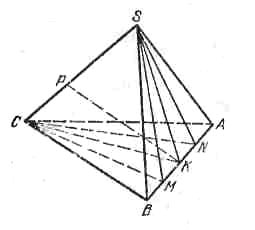
Пирамиду SPMN можно достроить до правильной призмы PMNSM1N1 так, что PMN и SM1N1 будут ее основаниями, a PS, ММ1, NN1, - ее боковыми ребрами.
Призма А1В1СА2В2S будет гомотетична призме PMNSM1N1 с центром в S и коэффициентом |CS| / |PS|.
Легко видеть, что искомая доля объема пирамиды SABC, находящаяся внутри призмы А1B1CA2B2S, равна отношению |MN| / |АВ|. Обозначим \(|АВ| = a\sqrtЗ,\;\; |CS| = 2a\). Найдем:
$$ |SK|=\frac{\sqrt{13}}{2}a, \;\;|CK|=\frac{3}{2}a,\;\;|PS|=\frac{5}{4}a, \\ |PK|=\frac{3\sqrt3}{4}a,\;\; |MN|=|PK|\frac{2}{\sqrt3}=\frac{3}{2}a, \;\;|MN|/|AB|=\frac{\sqrt3}{2} $$Ответ: \(\frac{\sqrt3}{2}\)
Похожие примеры: