В правильной четырехугольной усеченной пирамиде с боковыми ребрами AA1, ВВ1, СС1, DD1 сторона верхнего основания A1B1C1D1 равна 1, а сторона нижнего основания равна 7. Плоскость, проходящая через ребро В1С1 перпендикулярно к плоскости AD1C, делит пирамиду на две части равного объема. Найти объем пирамиды.
Пусть плоскость, проходящая через В1С1, пересекает АВ и DC в точках К и I. (рис.).
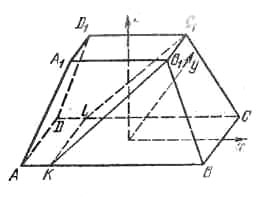
По условию, объемы многогранников AKLDA1B1C1D1 и КВСLВ1С1 равны. Применим к ним формулу Симпсона (\(V=\frac{h}{6}(S_1+S_2+4S)\)), обозначив |АК| = |DL| = a. Поскольку высоты этих многогранников равны, получим для a уравнение
$$ 7a+1+4\frac{(a+1)}{2}\cdot\frac{(7+1)}{2} = (7-a)7+4\frac{(7-a)}{2}\cdot\frac{(7+1)}{2} $$откуда a = 16/5.
Обозначим высоту пирамиды через h. Введем систему координат, взяв ее начало в центре ABCD, оси x и y параллельными АВ и ВС. Точки A, C и D1 будут иметь координаты \((-\frac{7}{2}, -\frac{7}{2}, 0),\;\;(\frac{7}{2}, \frac{7}{2}, 0),\;\;(-\frac{1}{2}, \frac{1}{2}, h)\)
Нетрудно найти уравнение плоскости ACD1: hx - hy + z = 0.
Плоскость KLC1B1 будет иметь уравнение lOhx - 8z + 3h = 0.
Нормальный вектор к первой плоскости n (h, -h, 1), ко второй m (10h, 0, -8). Условие их перпендикулярности даст нам
$$ 10h^2 - 8 = 0,\;\; h=\frac{2\sqrt5}{5} $$Объем пирамиды равен \(\frac{38\sqrt5}{5}\).