Основанием прямой призмы ABCDA1B1C1D1 служит равнобочная трапеция ABCD, в которой AD параллельна ВС, |AD|/|ВС| = n, n > 1. Через ребра AA1 и BC проведены плоскости, параллельные диагонали B1D; через ребра DD1 и B1С1 проведены плоскости, параллельные диагонали А1С. Определить отношение объема треугольной пирамиды, ограниченной этими четырьмя плоскостями, к объему призмы.
Плоскость, проходящая через АА1 параллельно B1D, будет параллельной плоскости DD1B1B. Точно так же плоскость, проходящая через DD1, параллельно А1С, будет параллельна плоскости АА1С1С.
С другой стороны, плоскости, проходящие через ребра ВС и В1С1, будут параллельны плоскостям AB1C1D и A1BCD1. Учитывая это обстоятельство, построим сечение наших многогранников плоскостью, параллельной основаниям и проходящей через середины боковых ребер, и плоскостью, проходящей через середины параллельных сторон оснований призмы (рис.).
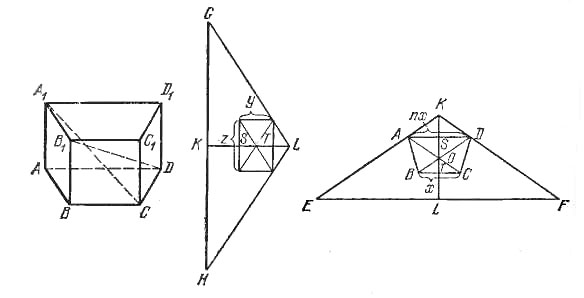
На рисунках L и К являются серединами противоположных ребер EF и HG треугольной пирамиды EFGH, сами ребра EF и HG перпендикулярны. Обозначая |ВС| = х, |AD| = nx, высоту трапеции ABCD через y, высоту призмы через z, найдем
$$ |KS|=|SO|=\frac{yn}{n+1},\;\;|TL|=\frac{y}{2}, \\ |KL|=y(\frac{3}{2}+\frac{n}{n+1}),\;\;|EF|=\frac{5n+3}{2}x,\;\;|GH|=\frac{5n+3}{n+1}z $$Объем призмы равен \(\frac{(n+1)xyz}{2}\). Объем треугольной пирамиды
$$ \frac{1}{6}|EF|\cdot|GH|\cdot|KL|=\frac{(5n+3)^3}{24(n+1)^2}xyz $$Ответ. \(\frac{(5n+3)^3}{24(n+1)^2}\)