В основании прямой призмы лежит прямоугольный треугольник ABC. Радиус окружности, описанной около него, равен R, катет АС стягивает дугу, равную 2β. Через диагональ боковой грани, проходящей через другой катет ВС, проведена плоскость перпендикулярно к этой грани, образующая с плоскостью основания угол β. Определить боковую поверхность призмы и объем отсеченной четырехугольной пирамиды.
Если катет AС (рис.) стягивает дугу, равную 2β , то ∠ AВС, как вписанный, опирающийся на эту дугу, будет равен β.
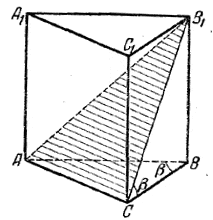
Плоскость, проходящая через диагональ В1С перпендикулярно к грани BB1C1C, должна пройти через AС, так как АС перпендикулярна к этой грани; линейный угол двугранного угла В1АСВ будет ∠ B1CB = β. Гипотенуза AВ есть диаметр описанной окружности и, следовательно, AB = 2R. Обозначим ВС = а, АС = b и АВ = с. Плоскость ACB1отсекает от призмы четырехугольную пирамиду B1AA1C1C. Так как объем пирамиды В1АВС равен 1/3 объема призмы, то объем оставшейся четырехугольной пирамиды равен 2/3 объема призмы. Если через V1 обозначим объе.м пирамиды B1AA1C1C, а через V - объем призмы, то
V1 = 2/3V = 2/3 • ab/2 • H = abH/3
Из \(\Delta\)ABC находим а и b, а из \(\Delta\)B1BC находим Н. Для боковой поверхности получим следующее выражение
Sбок. = (2R cos β + 2R sin β + 2R)•2R cos β tg β = 4R2 sin • (cos β + sin β + 1).
Выражение в скобках можно привести к виду, удобному для логарифмирования:
cos β + sin β + 1 = (1 + cos β) + sin β = 2 cos2 β/2 + 2 sin β/2 cos β/2
= 2 cos β/2 (cos β/2 + sin β/2 ) = 2 cos β/2 sin [(90° -
β/2 ) + sin β/2] =
= 2 cos β/2 • 2 sin 45° cos (45° - β/2 ) = 2√2 cos β/2 cos (45° - β/2).
Ответ: Sбок. = 8 √2 R2 sin β cosβ/2 cos(45° - β/2)
V1 = 4/3 R3 sin β sin 2β.