Основанием пирамиды служит трапеция, в которой боковые стороны и меньшее основание равны между собой, большее основание равно а и тупой угол трапеции равен α. Все боковые ребра пирамиды образуют с плоскостью основания угол β. Определить объем пирамиды.
Высота ЕО (рис., а) проходит через центр О окружности, описанной около трапеции ABCD.
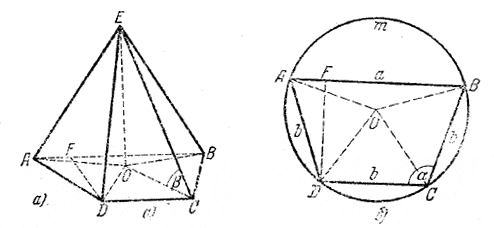
Дуги AD, DC и СВ - (рис., б) равны (так как по условию стороны AD, DC и СВ равны), причем ∠ B =180° - α измеряется половиной дуги ADC.
Значит, дуги AD, DC и СВ содержат по 180°- α; следовательно, дуга АmВ содержит 360° - 3 (180° - α) =3α - 180°. Из треуголышка АОВ, где АВ = а, находим
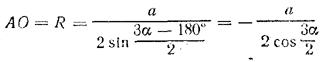
( величина cos 3α/2 отрицательна, ибо α - тупой угол, так что 135° < 3α/2 < 270° ).
Из треугольника ODC находим
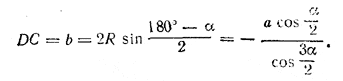
Из треугольника ADF, где AD = b и ∠ A = 180° - α, находим высоту трапеции
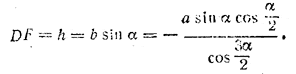
Из треугольника ВОЕ (см. рис., а), где OB = R и ∠ OВЕ = β, находим H = R tg β .
Площадь основания
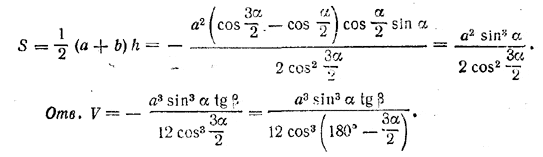
Похожие примеры: