Доказать, что, по крайней мере, одно из оснований перпендикуляров, опущенных из произвольно взятой внутренней точки выпуклого многоугольника на его стороны, лежит на самой стороне, а не на ее продолжении,
Пусть М — внутренняя точка выпуклого многоугольника, а АВ — его сторона, наименее удаленная от М. Докажем, что основание перпендикуляра Р, опущенного из М на АВ, лежит на АВ, а не на ее продолжении.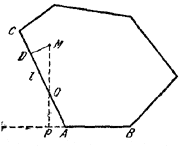
Действительно, если Р лежит вне АВ, то МР пересечет некоторую сторону l многоугольника в точке Q, причем, в силу выпуклости многоугольника, MQ < МР. Но расстояние DM от М до l меньше MQ, а значит и меньше МР, что противоречит выбору стороны АВ.
Похожие примеры: