Доказать, что биссектрисы внутренних углов параллелограмма в пересечении образуют прямоугольник, диагонали которого равны разности соседних сторон параллелограмма.

Пусть AA₁, BB₁, CC₁, DD₁ — биссектрисы внутренних углов параллелограмма ABCD, образующие в пересечении четырехугольник PQRS.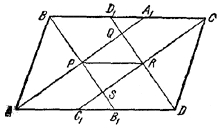

Очевидно, ВВ₁ || DD₁ и АА₁ || СС₁. Кроме того,

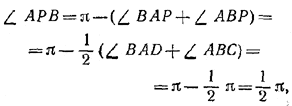
так что PQRS — прямоугольник. Треугольники BAB₁ и CDC₁ — равнобедренные, так как в них биссектрисы перпендикулярны основаниям. Поэтому BP = PB₁, D₁R = RD и, следовательно, PR || AD.

Таким образом, PRDB₁ — параллелограмм и

PR = B₁D = AD — AB₁ = AD — AB.