Доказать, что любой выпуклый четырехгранный угол можно пересечь плоскостью так, чтобы в сечении получился параллелограмм.
Пусть дан выпуклый четырехгранный угол с вершиной S.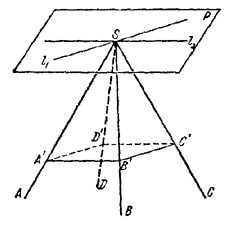
Продолжим плоскости BSC и ASD до их пересечения по прямой l1. Плоскости ASB и DSC продолжим до пересечения по прямой l2. Прямые l1 и l2, очевидно, не совпадают (в противном случае все грани при продолжении проходили бы через одну прямую).
Обозначим через Р плоскость, содержащую прямые l1 и l2. Легко показать, используя выпуклость четырехгранного угла, что плоскость Р имеет с данным углом лишь одну общую точку пересечения S, так что весь угол располагается по одну сторону от плоскости Р (впрочем, этот факт почти очевиден).
Покажем теперь, что всякая пересекающая угол плоскость, параллельная плоскости Р, образует с ним в сечении параллелограмм. В самом деле, такая плоскость пересечет, в силу сказанного, все четыре ребра четырехгранного угла. Обозначив соответствующие точки пересечения через А', В', С', В', заметим, что A'D' || В'С', так как оба эти отрезка порознь параллельны l1, по аналогичной причине А'В' || D'C'.
Следовательно, четырехугольник A'B'C'D' - параллелограмм, что и требовалось доказать.