Четыре шара, центры которых не лежат в одной плоскости, касаются попарно друг друга. Каждые два из них определяют плоскость, перпендикулярную к их линии центров и касающуюся обоих шаров. Доказать, что возникающие таким образом шесть плоскостей имеют общую точку.

Обозначим через О₁, О₂, О₃, О₄ центры данных шаров и через P_ik - общую касательную плоскость для шаров с центрами О_i и O_k (i < k). Таких плоскостей всего шесть: Р₁₂, Р₁₃, Р₂₃, P₁₄ , P₂₄, P₃₄.

Сначала докажем, что плоскости Р₁₂, Р₁₃ и Р₂₃ пересекаются по одной прямой. Действительно, каждая из этих плоскостей перпендикулярна к плоскости О₁О₂О₃, так как она перпендикулярна к линии центров разделяемых ею шаров, лежащей в этой плоскости.

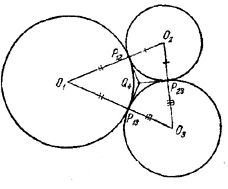
Кроме того, легко видеть, что рассматриваемые плоскости (рис.) проходят через точку Q₄ пересечения биссектрис \(\Delta\)О₁О₂О₃. Таким образом, плоскости Р₁₂, Р₁₃ и Р₂₃ действительно пересекаются по некоторой прямой, которая, как мы попутно установили, перпендикулярна к плоскости центров О₁О₂О₃ и проходит через центр вписанной в треугольник О₁О₂О₃ окружности. Обозначим эту прямую через L₄.

Совершенно так же доказывается, что плоскости Р₂₃ , Р₁₄ и Р₃₄ определяют общую им прямую L₁, перпендикулярную к плоскости треугольника О₂О₃О₄ и проходящую через центр вписанной в него окружности п т. д.

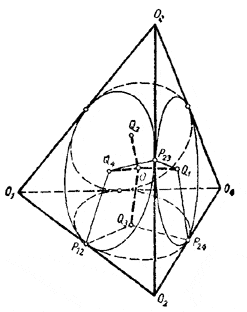
В результате мы приходим к следующей задаче (рис.): в каждую грань треугольной пирамиды О₁О₂О₃О₄ вписана окружность и через ее центр проведен перпендикуляр к грани. Нужно доказать, что все четыре перпендикуляра L₁, L₂, L₃ и L₄ имеют общую точку, если известно, что точки касания двух окружностей с одним и тем же ребром совпадают.

Этот факт почти очевиден. Обозначим через О точку пересечения прямых L₁ и L₄; последние пересекаются, так как лежат в одной плоскости Р₂₃ и не параллельны. Докажем теперь, что прямые L₃ и L₂ также проходят через точку О. Действительно, точка О лежит на линии пересечения плоскостей Р₁₂ и Р₂₄, так как прямая L₄ принадлежит плоскости Р₁₂, а прямая L₁-плоскости Р₂₄. Но линия пересечения Р₁₂ и Р₂₄ есть прямая L₃. Следовательно, L₃ проходит через точку О. Аналогично показываем, что прямая L₂ проходит через точку О.