Доказать, что если в треугольной пирамиде сумма длин любой пары противоположных ребер одна и та же, то вершины этой пирамиды являются центрами четырех шаров, попарно касающихся друг друга.

Если даны три точки А, В, С, не лежащие на одной прямой, то эти точки служат центрами трех шаров, попарно касающихся друг друга. Действительно, если Р-точка пересечения биссектрис \(\Delta\)ABC и Р₁, Р₂, Р₃ - основания перпендикуляров, опущенных из Р соответственно на стороны АВ, ВС и СА, то

АР₁ = АР₃, ВР₁ = ВР₂, СР₂ = СР₃

и шары с центрами А, В, С и радиусами, соответственно равными

r_А = АР₁, r_B = ВР₂, r_C = CP₃,

попарно касаются друг друга.

Пусть ABCD-данная пирамида (рис.).

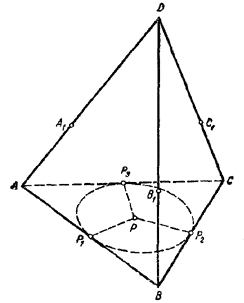
Рассмотрим три шара радиусов r_А, r_B, r_C с центрами в А, В, С, попарно касающихся друг друга. Обозначим через A₁, B₁ и С₁ точки, в которых поверхности шаров пересекаются с ребрами AD, BD и CD, и докажем, что A₁D=B₁D = C₁D.

По условию задачи

AD + BC = BD + AC.

По построению

AD = r_А+A₁D; BC = r_B + r_C ;

BD = r_B+ B₁D; AC = r_A + r_C.

Подставив четыре последних выражения в предыдущее равенство, получим:

A₁D = B₁D.

Аналогично, используя равенство

BD + AC = CD + AB,

найдем:

B₁D = C₁D

Следовательно, шар с центром D и радиусом

r_D = A₁D = B₁D = C₁D

касается каждого из первых трех шаров, а значит, все четыре построенных шара касаются попарно друг друга.