Определить угол при вершине в осевом сечении конуса, описанного около четырех равных шаров, расположенных так, что каждый касается трех других.
Центры О1,О2,О3,О4 четырех шаров, должны находиться .на расстоянии 2r друг от друга (см. предыдущую задачу). Значит, фигура О1О2О3О4 - правильный тетраэдр с ребром 2r. Конус АСВ (рис.) , описанный около четырех шаров, касается одного из них O4 по окружности NT, а каждого из трех остальных (например шара O1) в двух точках: одна из них, К, лежит на основании, другая, М - на боковой поверхности.
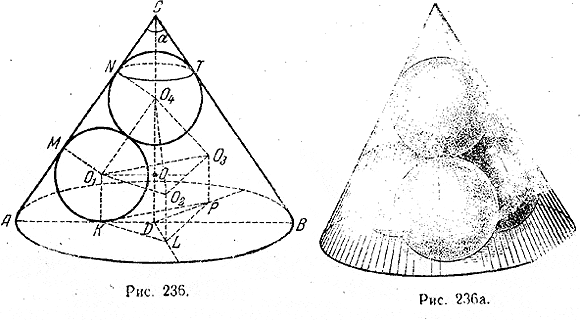
Ось конуса совпадает с высотой O4O тетраэдра. Центр O1 лежит в плоскости осевого сечения ACD, проходящего через точку касания М (ибо прямая О1М перпендикулярна к общей касательной плоскости конуса и шара, а плоскость осевого сечения ACD перпендикулярна к этой касательной плоскости). Значит, плоскость ACD пересекает шар О1 по большому кругу; шар О4 она пересекает тоже по большому кругу, и образующая АС есть общая касательная этих больших кругов.
Следовательно, AC || O1O4 и ∠ O1O4O = ∠ ACD= α/2 (α - искомый угол при вершине С осевого сечения). Значит, ![]()
Но O1O4 = 2r, а отрезок OO1 (радиус круга, описанного около треугольника O1O2O3) равен ![]() Получаем sin α/2= 1/√3
Получаем sin α/2= 1/√3
Отсюда можно найти cos α = cos2 α/2 - sin2 α/2 = 1/3.
Ответ: α = 2 arc sin 1/√3 = arc cos 1/3