Все три плоских угла некоторого трехгранного угла являются острыми. Один из них равен α; двугранные углы, прилежащие к этому плоскому углу, равны, соответственно, β и γ. Найти два других плоских угла.
Из некоторой точки S, отличной от вершины С и лежащей на том из ребер трехгранного угла, которое не является стороной плоского угла α, опустим перпендикуляры SB и SD на стороны указанного плоского угла и перпендикуляр SA на соответствующую грань.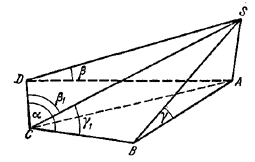
Обозначим искомые углы через β1 и γ1:
∠SCB = γ1, ∠SCD = β1.
Пусть, далее, ∠АСВ = α', ∠ACD = α". Полагая СА = а, из прямоугольных треугольников СВА, SBA и SBC находим:
![]()
Аналогично получаем:
tgβ1 = sec β tg α".
Задача свелась, следовательно, к нахождению tg α' и tg α". Имеем
α' + α" = α
Вычисляя разными способами отрезок SA, находим:SA = a sin α' tg γ
и
SA = a sin α"tg β.
Отсюда sin α' = sin α" tg βctg γ и, следовательно,
![]()
В результате, разделив на cos α' обе части последнего равенства, получаем:
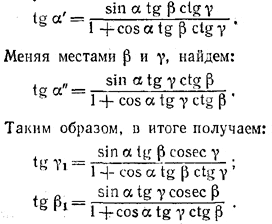
Похожие примеры: