Даны три плоских угла трехгранного угла SABC: ∠BSC= α; ∠CSA =β; ∠ASB = γ. Найти двугранные углы этого трехгранного угла.
Обозначим двугранные углы при ребрах SA, SB, SC (рис.) через φA , φB , φC.
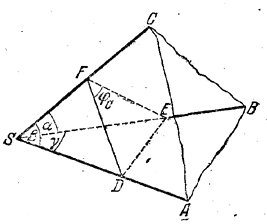
Проведем через какую-либо точку ребра SC плоскость DFE, перпендикулярную к SF. Тогда ∠DFE = φC. Определяем ED2 из треугольника EFD и из треугольника ESD, a затем приравниваем полученные выражения. Находим
FE2 + FD2 - 2 • FE • FD- cos φC = SE2 + SD2 - 2 • SE • SD • cos γ.
Отсюда
2 • FE • FD- cos φC = 2 • SE • SD • cos γ - (SE2-FE2) - (SD2- FD2),
т. е.
2 • FE • FD- cos φC = 2 • SE • SD • cos γ - 2 • SF2.
В это равенство подставляем
FE = SF• tg α ;
FD = SF• tg β;
SE = SF/cos α
и
SD = SF/cos β
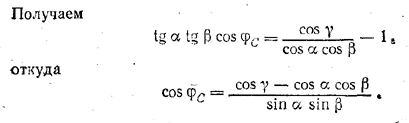
Аналогично найдем соs φA и cos φB .
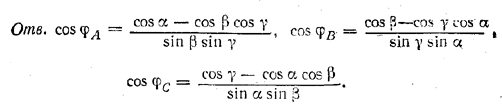
Похожие примеры: