Даны две скрещивающиеся прямые, наклоненные друг к другу под углом φ и имеющие общий пересекающий их перпендикуляр PQ = h. На этих прямых даны две точки А и В, из которых отрезок PQ виден под углами αи β. Определить длину отрезка АВ.

На рис. PQ изображает общий перпендикуляр к скрещивающимся прямым LL’ и ММ’. Чтобы получить угол, под которым отрезок PQ виден из точки А, нужно провести луч АР; тогда ∠ PAQ = α. Аналогично ∠ PBQ = β .

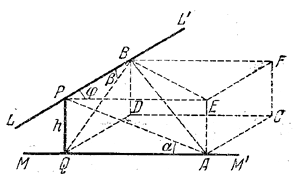
Проведем через точку Р прямую РЕ, параллельную ММ’. Тогда угол между прямыми MM’ и LL’ есть (по определению) угол φ = ∠ EPB. Опустим из А перпендикуляр АЕ на прямую РЕ и проведем АВ (все остальные линии, дающие изображение параллелепипеда, ребрами которого являются PQ, QA и РВ, проведены лишь для наглядности чертежа). Из прямоугольного треугольника BPQ находим

PB = PQ ctg β = h ctg β.

Аналогично

PE = QA = h ctg α.

Далее,

BE² = PB² + PE² -2 •PB•PE cos φ = h² (ctg² α + ctg² β-2 ctg α ctg β cos φ).

Прямая АЕ перпендикулярна к плоскости ЕРВ, так как она параллельна прямой PQ, являющейся общим перпендикуляром для прямых РВ и РЕ. Из прямоугольного треугольника AЕВ находим

AB²=AE² + BE² = h² + BE².

Ответ: AB² = h² ( 1 + ctg² α + ctg² β-2 ctg α ctg β cos φ)