На ребре двугранного угла дан отрезок АВ. В одной из граней дана точка М, в которой прямая, проведенная из точки А под углом α к АВ, пересекает прямую, проведенную из В перпендикулярно к АВ. Определить величину двугранного угла, если прямая AM наклонена ко второй грани двугранного угла под углом β.
Пусть точка М лежит на грани Q (рис.).
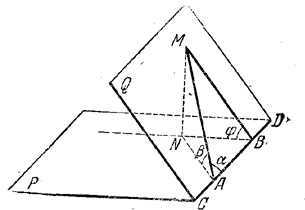
По условию прямая AM образует с АВ угол α, а прямая, MB перпендикулярна к АВ. Проведем через ВМ плоскость MBN, перпендикулярную к ребру, и опустим из точки М на BN перпендикуляр MN. Прямая MN перпендикулярна также и к NA и ∠ MAN = β (доказать!). Имеем также φ =∠ NBM. Угол φ мы найдем из треугольника NBM, где MN=AM • sin β (из треугольника ANM) и BM=AM • sin α (из треугольника AMВ). Получаем
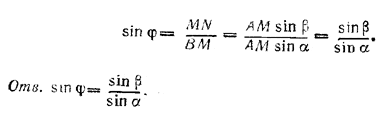
Похожие примеры: