Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда наклонены к плоскости его основания под углами α и β . Найти угол между этими диагоналями.

Угол между непересекающимися диагоналями BA₁ и AD₁ (рис.) равен углу φ = ∠A₁BC₁ между ВА₁ и прямой ВС₁ параллельной AD₁.

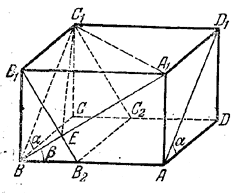
Имеем ∠CBC₁=∠DAD₁ = α и ∠ABA₁ = β. Для определения угла φ находим A₁C₁² сначала из треугольника A₁BC₁ (по теореме косинусов), а затем из прямоугольного треугольника A₁B₁C₁ и приравниваем найденные выражения. Получаем

ВА₁² + ВС₁² - 2 • BA₁ • BC₁ • cos φ = В₁А₁² + В₁С₁²

Отсюда

2 • BA₁ • BC₁ • cos φ = (ВА₁² - В₁A₁²) + (ВC₁² - В₁С₁²) = 2• BB₁².

B это равенство подставляем

(из треугольника BAA₁) и . Получаем

cos φ = sin α sin β.

Другой спocоб. Через ребро B₁C₁ проведем плоскость B₁C₁B₂C₂, перпендикулярную к BA₁(это возможно, так как B₁C₁⊥BA₁). Пусть Е - точка пересечения прямых BA₁ и B₁B₂. Из прямоугольного треугольника ВС₁Е находим BE = BC₁ cos φ , a из прямоугольного треугольника ВВ₁ Е, где ∠B₁BE = 90° - β, имеем

BE - BB₁ • cos(90° - β) = BB₁ • sin β.

Отрезок BB₁ выразим через ВС₁ из треугольника BB₁C₁, где ∠B₁BC₁= 90°- α. Получим BB₁ = BC₁ sin α и, значит,

BE = ВС₁ • sin α sin β.

Приравнивая два выражения отрезка BE, получаем

ВС₁ • cos φ = ВС₁ • sin α sin β.

Ответ: cos φ = sin α sin β.