В правильной шестиугольной пирамиде с плоским углом при вершине, равным α, проведено сечение через наибольшую диагональ основания под углом β к нему. Найти отношение площади сечения к площади основания.

Пусть S - вершина пирамиды, SO-высота, BN = NC.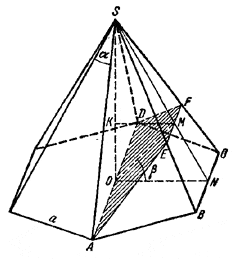

Обозначим сторону основания пирамиды через а. Временно положим ^SM/_SN= λ. Тогда из подобия треугольников легко находим, что

а из \(\Delta\)МКO получаем

Площадь сечения равна

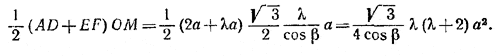
Площадь основания, как площадь правильного шестиугольника со стороной а, равна , а искомое отношение площадей равно

Следовательно, задача сводится к нахождению λ.

Для этой цели положим ∠SNO = φ . Тогда по теореме синусов из \(\Delta\)SOM получим: