Через вершину правильной треугольной пирамиды и середины двух сторон основания проведена плоскость. Определить площадь сечения и объемы частей данной пирамиды, на которые она разделена сечением, зная сторону а ее основания, и угол α, образованный сечением с основанием.
В сечении получаем треугольник DKN (рис.).
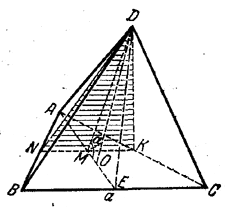
Как в задаче 125, докажем, что плоскость AED перпендикулярна к стороне ВС. Значит, она перпендикулярна и к средней линии KN. Следовательно, ∠ DME - линейный угол данного двугранного угла α.
Из треугольника OMD, где ОМ= 1/6 АЕ = 1/6 • a√3/2, находим
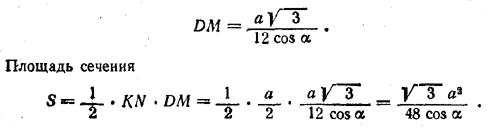
Площадь основания пирамиды DAKN вчетверо меньше площади основания пирамиды DABC, а высота у них общая. Поэтому объем V1 пирамиды DAKN равен 1/4V, где V-объем пирамиды DABC. Следовательно, объем пирамиды DKNBC V2 = 3/4 V. Объем V равен
V = 1/3 • Socн. • H = 1/3 • √3/4 a2 • .a√3/12 tg α
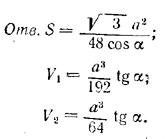
Похожие примеры: