Через вершину правильной четырехугольной пирамиды под углом φк основанию пирамиды проведена плоскость параллельно стороне основания. Сторона основания пирамиды равна а, а плоский угол при вершине пирамиды равен α. Найти площадь сечения пирамиды.
Прямая MN (рис.), по которой плоскость основания пересекается с плоскостью сечения, параллельна ВС.
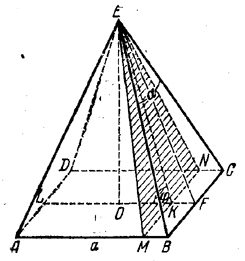
Чтобы построить угол φ, проведем OF || AB и соединим точку K, где OF встречает MN, с E. Тогда ∠ OKE = φ (доказать все это).
Площадь сечения S= 1/2 • МN • KE, где MN = a и KE = H/sin φ . Высота Н определяется из треугольника EOF, где OF= a/2 и FE = a/2 ctg α/2 (из треугольника EBF). Получаем
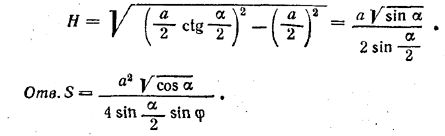
Похожие примеры: