В правильной четырехугольной пирамиде через вершину основания проведена плоскость, перпендикулярная к противоположному боковому ребру. Определить площадь сечения, если сторона основания пирамиды равна а, а боковое ребро наклонено к плоскости основания под углом φ (φ > 45° доказать это).

Проводим прямую CM (рис.), изображающую перпендикуляр, опущенный из С на АЕ.

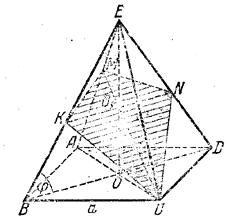
Через точку О₁ где СM встречает EO, проводим KN||BD. Четырёхугольник KCNM изображает сечение. Доказательство следует из нижеприводимого решения.

Решение. Так как плоскость KCNM перпендикулярна к ребру АЕ, то стороны МК и МN, а также диагональ СМ сечения KCNM перпендикулярны к АЕ. Так как диагональ СМ лежит в плоскости равнобедренного треугольника AЕС, то она пересекает прямую EO, являющуюся высотой этого треугольника. С другой стороны, диагональ KN, лежащая в плоскости треугольника BED (и, как сейчас будет доказано, параллельная основанию BD этого треугольника), тоже пересекает прямую ЕО, являющуюся высотой треугольника BED. А так как плоскость KCNM имеет с прямой ОЕ только одну общую точку О₁, то в этой точке диагонали KN и МС пересекаются друг с другом.

Плоскость KCNM перпендикулярна к ребру АЕ; потому углы ЕМК и EMN - прямые. Прямоугольные треугольники ЕМК и EMN равны (доказать!); следовательно, MK=MN и EK=ЕN. Из последнего равенства вытекает, что KN||BD и что KО₁ = О₁N. Следовательно, диагонали МС и KN взаимно перпендикулярны и, значит, S_cеч. = ¹/₂МС • KN.

Диагональ МС находим из прямоугольного треугольника АМС, где
∠ CAM = φ и AC = a√2 . Получаем МС = a√2 sin φ.

Диагональ KN находим из равнобедренного треугольника KEN, где ∠ EKN = φ. Имеем КN = 2 • О₁E • ctg φ, где О₁E = ОЕ - ОО₁ . Отрезок ОЕ определяется из треугольника АОЕ (или ВОЕ); находим . Отрезок же OO₁ определяется из треугольника ОСО₁ , где ∠ OCO₁ = 90°- ^MAС = 90° - φ.

Находим

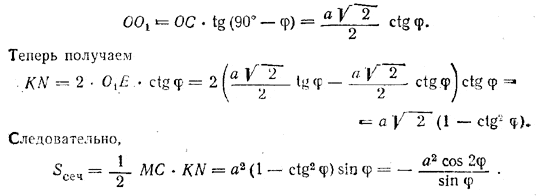
Замечание. Для того чтобы плоскость KCNM, перпендикулярная к АЕ, дала бы сечение пирамиды, нужно, чтобы точка М ее пересечения с прямой АЕ лежала на отрезке АЕ (а не на его продолжении), а для этого угол AЕС должен быть острым,
т.е. ∠ AEС= 180° - 2φ < 90°. Следовательно, φ > 45°, а поэтому cos 2φ есть величина отрицательная.