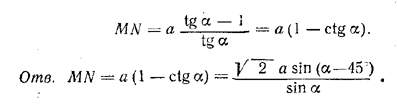В правильной четырехугольной пирамиде сторона основания равна а, а двугранный угол при основании равен α. Через две противоположные стороны основания пирамиды проведены две плоскости, пересекающиеся взаимно под прямым углом. Определить длину линии их пересечения, заключенную внутри пирамиды, если известно, что она пересекает ось пирамиды.

Сделав изображение пирамиды EHPGQ (рис.), изображаем прямую MN, по которой пересекаются плоскости, она параллельна стороне HP и пересекает ось ОЕ в точке В.

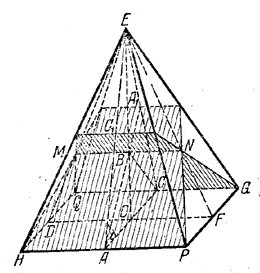
Концы М и N отрезка MN лежат на апофемах ED и EF. Проведя PN и GN, HМ и QM, получаем изображение плоскостей, пересекающихся по MN. Ответим точки А₁ и С₁, лежащие на пересечении АВ и СВ с апофемами ЕА и ЕС (А и С- середины HP и QG). Угол ABC - линейный угол получившегося двугранного угла. По условию ∠ ABC = 90°, т. е. треугольник AВС - равнобедренный прямоугольный и

ВО = АО = ^a/₂

Решение. Из подобия треугольников EMN и EDF, где DF = a, имеем
MN = а • ^EB/_EO . Угол ОАЕ есть линейный для двугранного угла α, так что
ЕО = АО • tg α = ^a/₂ • tg α. Кроме того, ЕВ = ЕО - ВО = ^a/₂ (tg α -1). Следовательно,