В правильной четырехугольной пирамиде двугранный угол при основании равен α. Через его ребро проведена плоскость, составляющая с основанием угол β. Сторона основания равна а. Определить площадь сечения.
Сечение BCC1B1 (рис.) есть трапеция (дoказать!).
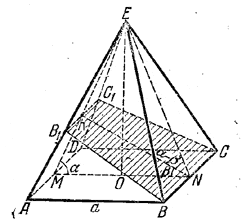
Проведем плоскость MNE (М и N - середины сторон AD и ВС). Она пересечет плоскость BCC1B1 по прямой NK (К - середина B1C1).
Имеем ∠NME = ∠MNE = α и ∠MNK = β (доказать!). Высота KN трапеции ВСС1В1 находится из треугольника KNM, где МN= а ∠MKN = 180°- (α + β). По теореме синусов ![]() т.е.
т.е. ![]()
Теперь находим верхнее основание В1С1 трапеции; из подобия треугольников ADE и B1С1Е имеем
![]()
Отношение KE/NE найдем из треугольника КNЕ, где ∠KNE = α - β, a ∠NKE = α + β (как внешний для \(\Delta\)KNM). Получаем
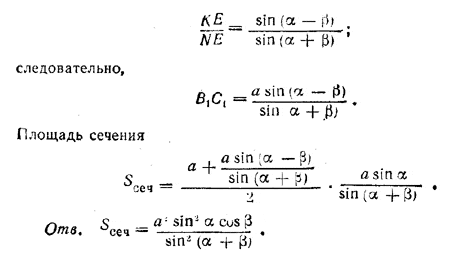
Похожие примеры: