Двугранный угол при боковом ребре правильной шестиугольной пирамиды равен φ. Определить плоский угол при вершине пирамиды.

Равнобедренные треугольники BMA и FMA (рис.) равны.

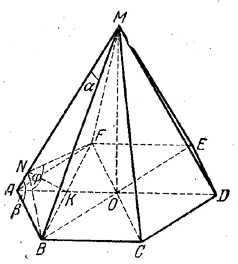
Поэтому их высоты, опущенные из вершин В и F, пройдут через одну и ту же точку N их общей стороны и будут равны: BN=FN. Угол BNF равен φ (доказать!).

Угол β = ∠ BAM выражается через искомый угол α = ∠BMA формулой

β = 90° - ^α/₂.

Найдем сначала тригонометрическую функцию угла β. Из прямоугольного треугольника ABN имеем sin β = ^BN/_a (а - сторона основания). Из равнобедренного треугольника BNF находим .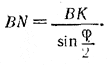

Но ВК = ^a√3/₂ (как высота равностороннего треугольника АВО).

Следовательно,

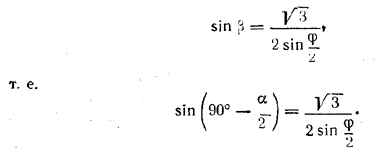
Замечание. Двугранный угол при ребре правильной шестиугольной пирамиды всегда больше, чем ∠ FAB (сравнить треугольники BNF и BAF), т. е. больше 120°. Поэтому величина 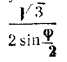всегда меньше единицы.