Пирамида имеет в основании правильный шестиугольник ABCDEF. Боковое ребро МА перпендикулярно к плоскости основания, а противоположное ему ребро MD наклонено к плоскости основания под углом α. Определить углы наклона боковых граней к плоскости основания.
Грани AMF и АМВ (рис., а), проходящие через ребро AM (перпендикулярное к плоскости ABCDEF), образуют с плоскостью основания прямые углы.
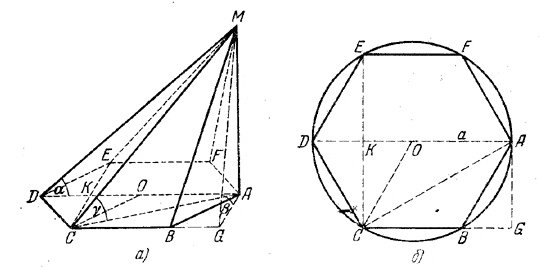
Найдем общую величину β углов, образуемых гранями EMF и СМВ с плоскостью основания. Опустим из А перпендикуляр AG на прямую СВ (изображение этой прямой должно быть параллельно СЕ, рис., б). Тогда β = ∠ AGM (доказать!).
Имеем tg β = H/AG , где AG = СК = a√3/2. (рис., б). Но из треугольника AMD имеем tg β = H/2a ; следовательно,
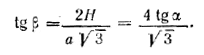
Так как AC⊥DC (доказать!), то γ = ∠ ACM есть линейный угол для двугранного угла, под которым грань DCM (и DEM) наклонена к плоскости основания. Из треугольника АСМ имеем tg γ = H/AC, где AС = а√3 (рис., б).
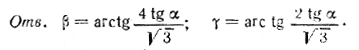
Похожие примеры: