Основанием прямого параллелепипеда служит ромб. Плоскость, проведенная через одну из сторон нижнего основания и противоположную сторону верхнего основания, образует с плоскостью основания угол β. Полученное сечение имеет площадь, равную Q. Определить боковую поверхность параллелепипеда.

Сечение есть параллелограмм A₁D₁CB (рис.).

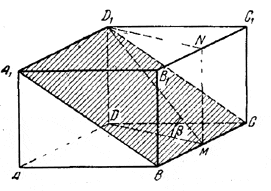
Чтобы изобразить линейный угол двугранного угла, образуемого сечением A₁D₁CB с плоскостью основания, проведем прямую DM, изображающую высоту ромба ABCD. Так как в натуре DM и DD₁ перпендикулярны к ребру AD, то плоскость DD₁NM перпендикулярна к AD, а значит, и к ВС. Эта плоскость пересекает плоскость сечения по прямой MD₁ так что

∠ D₁MD = β

Решение. Боковая поверхность состоит из четырех равных прямоугольников (так как основание - ромб). Площадь боковой грани A₁D₁DA равна S₁= A₁D₁ • DD₁, а площадь сечения равна Q = A₁D₁ • D₁M. Из треугольника DMD₁ имеем DD₁ = D₁M sin β; поэтому S₁= Q sin β.

Ответ: S_бок. = 4Q sin β.